A Library is a Language is a Library
2017-10-17
Designing a software library is a popular activity. Not only is it a welcome contribution but it is considered something readily achievable. Designing an API, i.e., the library’s appearance to the user, is no black art and design decisions are based on functionality rather than to personal tastes or preferences. Often, the purpose of a new library is to outperform another library and a whole category of research papers is dedicated to performance comparisons of different algorithm implementations (i.e., libraries).
In contrast, the design of a programming language is viewed as a black art. Relatively few people have attempted to create a language, and even fewer people have succeeded. The contribution of a new programming language is often viewed as an annoyance because in the best case one has to relearn programming and in the worst case the reward for learning the new language is nil. Many aspects of language design express tastes and preferences and the usefulness of a language cannot be captured by considering only performance or other tangible features.
In essence, coming to use a new language is associated with a high upfront investment and unforeseeable risks, whereas coming to use a new library is associated with a negligible cost and predictable risks. I think, both preconceptions are somewhat false and yet they reflect the experience of many programmers: The highest cost ever incurred is the first programming language one had to learn. And the greatest relief ever experienced is the effortless combination of a few libraries to form something new and useful. Accordingly, we are told to create libraries instead of languages or that there are already too many programming languages out there. Fred Brooks called on a moratorium on new programming languages in a talk he gave in 1993.
However, the design of a programming language and the design of a library have a lot in common. The signatures of a library’s API functions are a lot like the syntax of a programming language. Calling a library’s API function is a lot like constructing an expression. Transforming data is a lot like reduction. In fact, Martin Fowler tells us that whenever we come across a domain-specific language implemented as an internal language in Ruby, Scala, or Lisp that is exactly what happens under the hood.
If that is so we can ask whether we can make better libraries by thinking of libraries as languages. Extensive research is available about the modeling of the syntax and semantics of programming languages. Can we use methods to model and analyze languages to model and analyze libraries? Can we come up with simpler and more expressive APIs? Can we reduce the contact surface for bugs and better understand what our libraries are supposed to do? The answer is yes, of course.
Example: A Zero-Order Logic
To demonstrate the point, let me introduce a working example: A zero-order logic. This is a logic with two truth values and some operators to combine simple truth values to propositions like negation (not), conjunction (and), or disjunction (or). Every proposition in such a logic can be evaluated to a truth value, i.e., it is either true or false.
In the following, we examine this zero-order logic in terms of a structural operational semantics and look at a small semantic model in Java that closely corresponds to this semantics.
A Language has a Syntax
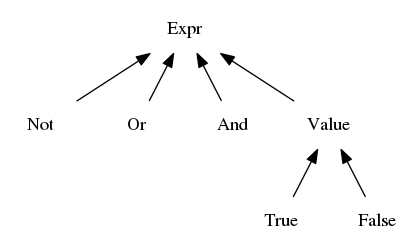
The first important observation is that a language has a syntax. By expressing this syntax in Backus-Naur form, we enumerate all ways to create an expression in the language. Let us do this for our zero-order logic:
When creating a library it helps to have an equivalent of such a syntax spec around. The first step to creating such a syntax representation in Java is to create an empty marker interface Expr. Later, we will create a class for each syntactic category we defined in the abstract syntax.
But for now, let us think about, how one would explore such a library, when seeing it for the first time. To find out, what ways exist to create expressions one would have to do two things: (i) finding out which classes implement Expr, and (ii) finding out which ways exist to construct each of these classes. Of course we can get such an overview by looking at the class hierarchy diagram of the Expr interface. But to understand, how each syntactic category is constructed, we still need to look at each of the constructors. To get all information in one place, let us create an additional interface Logic that enumerates all ways to construct an expression.
package logic;
public interface Logic {
public Expr t();
public Expr f();
public Expr not( Expr a );
public Expr and( Expr a, Expr b );
public Expr or( Expr a, Expr b );
}
In contrast, the Logic interface is a concise overview of all the ways we can construct an expression, just like a syntax spec in Backus-Naur form.
Math is Immutable
We continue by creating the classes True, False, Not,:code:And, and Or which all implement the empty marker interface Expr. The classes True and False just stay empty but the other three contain private fields representing the according subexpressions. It is good practice to mark these private fields as final. This allows us to reuse expressions without having to worry that they might change accidentally.
package logic;
public class Not implements Expr {
private final Expr a;
public Not( Expr a ) {
if( a == null )
throw new IllegalArgumentException( "Argument must not be null." );
this.a = a;
}
public Expr getA() { return a; }
}
Object Orientation is a False Friend
Before we continue, let us make a distinction between value and non-value expressions. An expression is a value if it has the following form:
There are several ways how to implement the distinction between expressions and values in an object oriented language like Java. The first possible approach is to create an empty marker interface Value that inherits from Expr. Accordingly, True and False are updated to implement Value. While this is the true lore of object orientation, note how this hierarchical definition differs from the way we defined e and v in the abstract syntax. Their definitions were independent and not hierarchical. Let’s take this independence serious and try to come up with an alternative way.
Distinguishing Values by making them part of the class hierarchy. Not recommended because the definition of expressions and values should be independent.
Another approach could be to extend the marker interface Expr to contain a method isValue. This way, the independence of the definition of expressions and the definition of values is conserved. However, now the value definition is smeared all over the code base. When we try to reason about the behavior of the library we might ask “Why is this a value?”. To find out, we have to visit a number of classes while in the language, the value definition is in one spot. Let’s take this collocation serious and come up with an alternative way.
Well, obviously what we want is a single function that takes an instance of Expr and returns a Boolean. Let’s add it to the implementation of the Logic interface.
package logic;
public class DynamicLogic implements Logic {
...
public boolean isValue( Expr e ) {
if( e instanceof True ) return true;
if( e instanceof False ) return true;
return false;
}
}
First Divide
Now, we are ready to describe how reduction is performed, i.e., how we come from a general proposition (an instance of Expr) to a truth value (an instance of either True or False). We do this by defining a notion of reduction. This is a set of reduction rules for non-value expressions, for which we assume, that all subexpressions are already values. Of these we have the following six:
Let us add a function step to the DynamicLogic class just as we did for isValue. By default, i.e., if no reduction rule applies, we want it to return null.
package logic;
public class DynamicLogic implements Logic {
...
public Expr step( Expr e ) {
if( e == null )
throw new IllegalArgumentException( "Argument must not be null." );
// add rules here
return null;
}
}
Now, one by one, we add an if clause for each of the rules in the notion of reduction. To keep it short I give only the first if clause here:
if( e instanceof Not ) {
Not n = ( Not )e;
if( n.getA() instanceof True )
return f();
}
This way each rule is enumerated one after the other. Note how each rule implementation is independent from each of the others. Moreover, each rule is simple. No recursion (so far), no visitor pattern, no [burrito](https://www.google.com/search?q=monads+are+burritos).
Then Conquer
Of course, the notion of reduction as presented here is insufficient to reduce complex expressions. We still need to add a few congruence rules to perform reduction on nested expressions. The following three congruence rules are needed:
Again, I’ll give the implementation only of the first rule here.
if( e instanceof Not ) {
Not n = ( Not )e;
if( !isValue( n.getA() ) )
return not( step( n.getA() ) );
}
The three congruence rules are added to the step function in the same way as the rules for the notion of reduction. Taken together, these nine rules define how reduction works. Unless an expression is a value there is always at least one rule that applies.
However, we are not done yet. Each rule takes only a single step in reduction. Next, we need to chain up reduction steps until a value results. We do this by creating a function eval, which we add to the DynamicLogic class:
package logic;
public class DynamicLogic implements Logic {
...
public Expr eval( Expr e ) {
Expr e1 = step( e );
return e1 == null ? e : eval( e1 );
}
}
And that’s it.
The simplicity we have achieved comes from two sources: (i) we have created a small number of functions with a clear and limited purpose, and (ii) we have defined all data transformations in terms of flat, simple, and independent rules (the notion of reduction).
In the process we ignored the object oriented convention to disperse information in classes and methods and instead concentrated relevant information in functions. Note, how this increases clarity.
Further, we ignored the possibility to mutate expressions in-place. Note, how this increases safety.
We have ignored coding patterns that are usually applied in this kind of situation, most prominently the visitor pattern. This simplifies debugging. Only if you have stepped through heaps and heaps of invocations of methods all named visit and accept you can appreciate this fact. Note how this makes the code testable: Write at least one unit test per rule!
We have made shameless use of reflection and downcasts, even if they are dangerous since downcasts explicitly sidestep Java’s type checker. But that just reflects Java’s poor job on dynamic dispatch.
The Big Picture
It may surprise you (or maybe it doesn’t) that this style of solving a problem is applicable in many situation one may encounter. For many data structures, one can sit down and write a syntax. For many algorithms, one can sit down and fray out simple, flat, and independent reduction rules.
For some well-studied text book algorithms it may be unnecessary to go that far. For such algorithms the gains in performance and memory saving would be squandered if we implement them as a language. However, I would presume that most problems that need solving do not appear in text books and are not well-studied.
Also, we have been very lax about the reasons why the result is the same no matter in which order we apply the reduction rules. Similarly, we just claimed that at the end of the reduction process there will always stand a value. While these things are known for our zero-order logic, they are far from self-evident in general. Great care must be taken to avoid mishaps here.
Post Scriptum
We have defined reduction as a relation, i.e., the smallest relation that fulfills all reduction rules, but have implemented reduction as a function. A well-known programming language that allows the formulation of reduction rules as relations is Prolog. So if you have had the feeling that object orientation is a limiting factor here and that a functional programming language might be better suited for the task of defining a language – logic programming is even better. But if you know what you are doing the actual programming language you use does not matter so much.
The equating of languages and libraries, as shown here, is also part of the agenda of the Racket community. We have come full circle. Not only can we design libraries like we design languages, with Racket, we can also come up with a small specialized language whenever we have written a library. Wouldn’t it be much better to teach people language design first and teach them programming later?